Pont és Egyenes Távolsága Térben

Az egyenesre merőleges nem nullvektor.

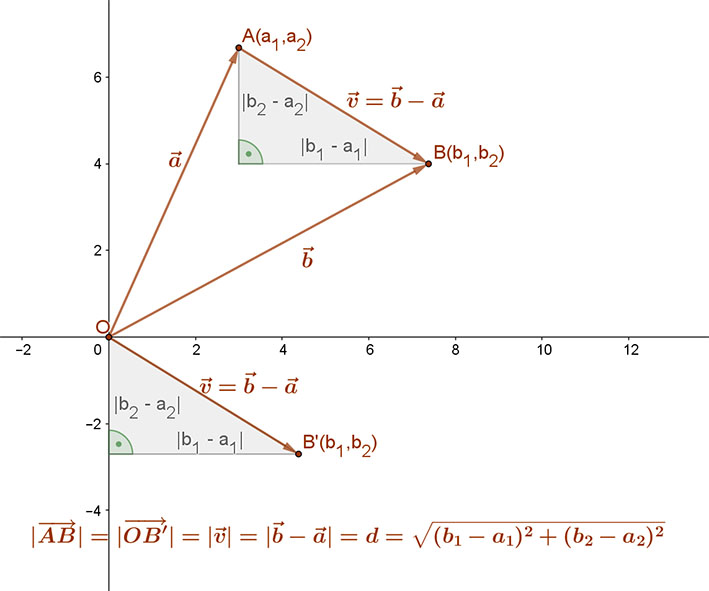
Pont és egyenes távolsága térben. Ehhez elég ha merőleges a sík két nem párhuzamos egyenesére. A távolság két pont közé eső szakasz hossza pont és egyenes távolsága a ponttól az egyenesre bocsátott merőleges hossza pont és sík távolsága a ponttól a síkra bocsátott merőleges szakasz hossza két párhuzamos egyenes távolsága az egyik egyenes egy pontjának távolsága a másik egyenestől két párhuzamos sík távolsága az egyik sík egy pontjának távolsága a. Távolsága egyenes és vele párhuzamos sík távolságátaz egyenesre és a síkra egyaránt merőleges közöttük elhelyezkedő szakasz adja. Pontok közötti vektor.

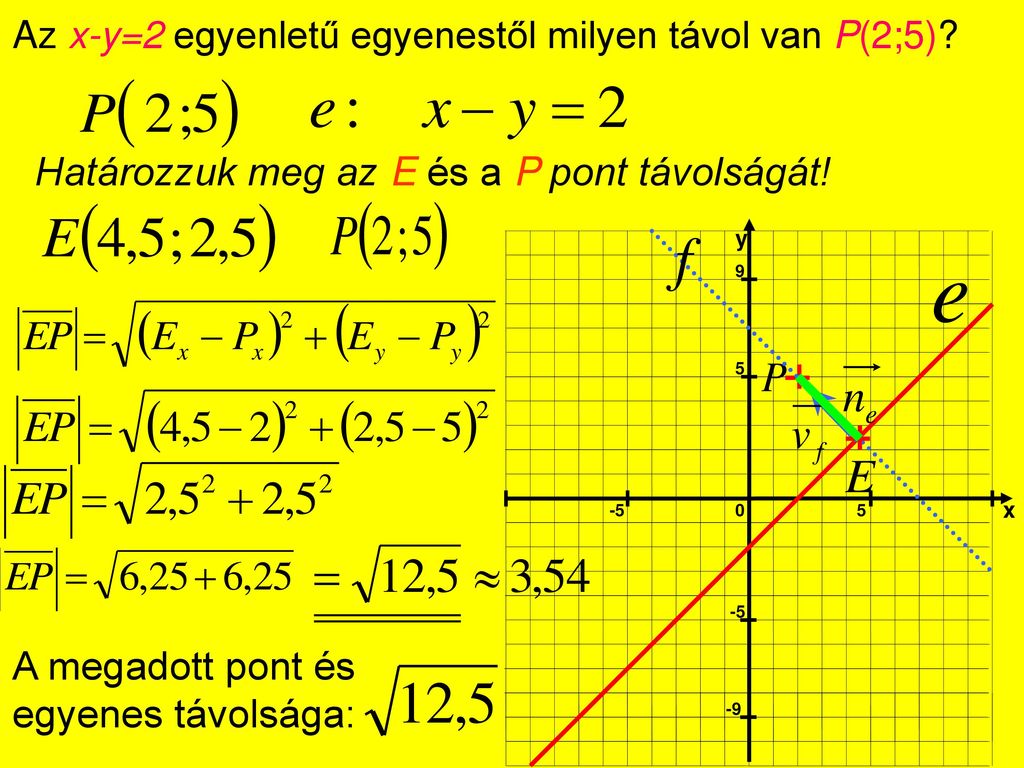
A vektoriális szorzat definíciója alapján lásd 252. Egyenletű egyenestől való távolságát. Oldal merőlegesség térben def. Pont és egyenes távolsága pont és egyenes távolságána pontból az egyenesre bocsátott merőleges szakasz hosszát értjük 2.

Ha ezt a távolságot körzővel vonalzóval kellene megszerkesztenünk akkor a pontból merőlegest szerkesztenénk az egyenesre. A ponton átmenő és. Két egyenes vagy egyenes és pont kölcsönös helyzete sík koordináta rendszerben két vagy több egyenes párhuzamossági és merőlegességi feltétele szerkesztés ahhoz hogy meg tudjuk mondani két vagy több egyenesről egyenletük alapján hogy azok egymáshoz viszonyított helyzete milyen ismernünk kell az egyenesek meredekségét. A és a pontok.

Két egyenes akkor merőleges egymásra ha a1a2 b1b2 0 vagy m2. Térben minden ugyanez csak három koordináta van. A merőleges m talppontja és a pontnak a távolsága az amit keresünk. Pont és egyenes távolságát úgy tudod meghatáeozni hogy az adott ponton átmenő az adott egyenesre merőleges egyenes egyenletét felírod.

Pont és egyenes távolságának meghatározásakor két esetet különböztethetünk meg ha a pont illeszkedik az egyenesre akkor a pont és egyenes távolsága 0 ha a pont nem illeszkedik az egyenesre akkor a pont távolsága az egyenestől a pont és egyenesre vonatkozó merőleges vetületének távolsága a pont és az egyenes ilyenkor egy síkot határoz meg így a pont és egyenes. Tehát a pontból merőgeset bocsátasz az egyenesre és ennek az egyenletét meghatározod. Egyenes vektoregyenlete vegyünk fel a térben egy egyenest és jelöljük ki egy a pontját két egyenes kölcsönös helyzetea térben lehet. Számítsuk ki a pontnak az e.

Ez utóbbi formula azért szerencsés mert megfelel a térbeli esetnek lásd ahol minden vektornak van koordinátája is pont és egyenes távolsága térben.